HEISENBERG UNCERTAINTY PRINCIPLE

the uncertainty principle states that the position and velocity cannot both be measured,exactly, at the same time (actually pairs of position, energy and time) uncertainty principle derives from the measurement problem, the intimate connection between the wave and particle nature of quantum objects the change in a velocity of a particle becomes more ill defined as the wave function is confined to a smaller region

Classical physics was on loose footing with problems of wave/particle duality, but was caught completely off-guard with the discovery of the uncertainty principle.The uncertainty principle also called the Heisenberg Uncertainty Principle, or Indeterminacy Principle, articulated (1927) by the German physicist Werner Heisenberg, that the position and the velocity of an object cannot both be measured exactly, at the same time, even in theory. The very concepts of exact position and exact velocity together, in fact, have no meaning in nature. Ordinary experience provides no clue of this principle. It is easy to measure both the position and the velocity of, say, an automobile, because the uncertainties implied by this principle for ordinary objects are too small to be observed. The complete rule stipulates that the product of the uncertainties in position and velocity is equal to or greater than a tiny physical quantity, or constant (about 10-34 joule-second, the value of the quantity h (where h is Planck's constant). Only for the exceedingly small masses of atoms and subatomic particles does the product of the uncertainties become significant. Any attempt to measure precisely the velocity of a subatomic particle, such as an electron, will knock it about in an unpredictable way, so that a simultaneous measurement of its position has no validity. This result has nothing to do with inadequacies in the measuring instruments, the technique, or the observer; it arises out of the intimate connection in nature between particles and waves in the realm of subatomic dimensions. Every particle has a wave associated with it; each particle actually exhibits wavelike behavior. The particle is most likely to be found in those places where the undulations of the wave are greatest, or most intense. The more intense the undulations of the associated wave become, however, the more ill defined becomes the wavelength, which in turn determines the momentum of the particle. So a strictly localized wave has an indeterminate wavelength; its associated particle, while having a definite position, has no certain velocity. A particle wave having a well-defined wavelength, on the other hand, is spread out; the associated particle, while having a rather precise velocity, may be almost anywhere. A quite accurate measurement of one observable involves a relatively large uncertainty in the measurement of the other.The uncertainty principle is alternatively expressed in terms of a particle's momentum and position. The momentum of a particle is equal to the product of its mass times its velocity. Thus, the product of the uncertainties in the momentum and the position of a particle equals h/(2) or more. The principle applies to other related (conjugate) pairs of observables, such as energy and time: the product of the uncertainty in an energy measurement and the uncertainty in the time interval during which the measurement is made also equals h/(2) or more. The same relation holds, for an unstable atom or nucleus, between the uncertainty in the quantity of energy radiated and the uncertainty in the lifetime of the unstable system as it makes a transition to a more stable state.

the wave nature to particles means a particle is a wave packet, the composite of many waves many waves = many momentums, observation makes one momentum out of many exact knowledge of complementarity pairs (position, energy, time) is impossible

The uncertainty principle, developed by W. Heisenberg, is a statement of the effects of wave-particle duality on the properties of subatomic objects. Consider the concept of momentum in the wave-like microscopic world. The momentum of wave is given by its wavelength. A wave packet like a photon or electron is a composite of many waves. Therefore, it must be made of many momentums. But how can an object have many momentums?Of course, once a measurement of the particle is made, a single momentum is observed. But, like fuzzy position, momentum before the observation is intrinsically uncertain. This is what is know as the uncertainty principle, that certain quantities, such as position, energy and time, are unknown, except by probabilities. In its purest form, the uncertainty principle states that accurate knowledge of complementarity pairs is impossible. For example, you can measure the location of an electron, but not its momentum (energy) at the same time.

complementarity also means that different experiments yield different results (e.g. the two slit experiment) therefore, a single reality can not be applied at the quantum level

A characteristic feature of quantum physics is the principle of complementarity, which "implies the impossibility of any sharp separation between the behavior of atomic objects and the interaction with the measuring instruments which serve to define the conditions under which the phenomena appear." As a result, "evidence obtained under different experimental conditions cannot be comprehended within a single picture, but must be regarded as complementary in the sense that only the totality of the phenomena exhausts the possible information about the objects." This interpretation of the meaning of quantum physics, which implied an altered view of the meaning of physical explanation, gradually came to be accepted by the majority of physicists during the 1930's.Mathematically we describe the uncertainty principle as the following, where `x' is position and `p' is momentum:

the mathematical form of the uncertainty principle relates complementary to Planck's constant knowledge is not unlimited, built-in indeterminacy exists, but only in the microscopic world, all collapses to determinism in the macroscopic world

This is perhaps the most famous equation next to E=mc2 in physics. It basically says that the combination of the error in position times the error in momentum must always be greater than Planck's constant. So, you can measure the position of an electron to some accuracy, but then its momentum will be inside a very large range of values. Likewise, you can measure the momentum precisely, but then its position is unknown.Notice that this is not the measurement problem in another form, the combination of position, energy (momentum) and time are actually undefined for a quantum particle until a measurement is made (then the wave function collapses). Also notice that the uncertainty principle is unimportant to macroscopic objects since Planck's constant, h, is so small (10-34). For example, the uncertainty in position of a thrown baseball is 10-30 millimeters. The depth of the uncertainty principle is realized when we ask the question; is our knowledge of reality unlimited? The answer is no, because the uncertainty principle states that there is a built-in uncertainty, indeterminacy, unpredictability to Nature.

Dual Nature of Radiation and Matter

The Photoelectric Effect

 When light of sufficiently small wavelength is incident on a metal surface, electrons are ejected from the metal. This phenomenon is called as 'photoelectric effect' and the ejected electrons are called as 'photoelectrons'.

Particle Nature of Light

     According to wave theory when light falls on a metal surface, energy is continuously distributed over the surface. All the free electrons receive light energy and when the energy received exceeds that of work function, an electron may escape the surface. If we user a low intensity source, it may take hours before an electron to come out.s

Photocells and their Application

     A photocell converts the change in the intensity of light into a change in the electric current. The diagram shows a photocell circuit. The cathode is made of photosensitive material.

Photo Voltaic Cell

     Photo voltaic cell converts light energy into electrical energy. It acts as a cell. It consists of a metal layer of copper over which a semiconductor layer of cuprous oxide coated with a thing film of silver or gold.

Photoconductive Cell

     The electrical resistance of a semiconductor depends on the intensity of the incident light. A photoconductive cell works on the above principle.

Applications of Photoelectric Cells

     Photocells are used in television camera to reproduce sound recorded on films, in counting devices, in burglar and fire alarms, to measure the temperature of stars, to study the spectrum of heavy bodies, to operate street light, to compare the illuminating powers of two sources, in photometers, for locating minor flaws in metallic sheets, to determine the opacity of solids and liquids, to control the temperature in chemical reactions and to determine the Planck's constant.

Matter Waves

     The suggestion that matter may have wave like properties was first put forwarded in 1924-1925 by Louis De Broglie. He argued that if light, which consists of waves according to classical picture, can sometimes behave like particles, then it should be possible for matter, which consists of particles to exhibit wave-like character under suitable circumstances.

De-Broglie Relationship

     De-Broglie noted that according to the theory of relativity, the role played by momentum 'P' and the energy 'E' of the particle is done by angular frequency 'w' and the propagation vector 'k' of a wave.

De-Broglie Wavelength of an Electron

     Similar to the crystal diffraction patterns produced by X-rays, even the beam of electrons of appropriate momentum could produce crystal diffraction pattern.s

Davison and Germer Experiment

     The first experimental proof of the wave nature of electron was demonstrated in 1927 by two American physicists C.J Davison and L.H Germer.

Elementary Idea of Electron Microscope

     In optical microscope, the ray of light can be bent by a lens system. By placing the object and the lens system in such a way, we control the direction of the ray to get a magnified image of the object.

Summary

     The phenomenon of interference, diffraction and polarization can be explained by the wave theory of light.

BOHR MODEL OF ATOM

The Bohr Model has an atom consisting of a small, positively-charged nucleus orbited by negatively-charged electrons. Here's a closer look at the Bohr Model, which is sometimes called the Rutherford-Bohr Model.

Overview of the Bohr Model

Niels Bohr proposed the Bohr Model of the Atom in 1915. Because the Bohr Model is a modification of the earlier Rutherford Model, some people call Bohr's Model the Rutherford-Bohr Model.

The modern model of the atom is based on quantum mechanics. The Bohr Model contains some errors, but it is important because it describes most of the accepted features of atomic theory without all of the high-level math of the modern version. Unlike earlier models, the Bohr Model explains the Rydberg formula for the spectral emission lines of atomic hydrogen.

The Bohr Model is a planetary model in which the negatively-charged electrons orbit a small, positively-charged nucleus similar to the planets orbiting the Sun (except that the orbits are not planar). The gravitational force of the solar system is mathematically akin to the Coulomb (electrical) force between the positively-charged nucleus and the negatively-charged electrons.

Main Points of the Bohr Model

• Electrons orbit the nucleus in orbits that have a set size and energy.
• The energy of the orbit is related to its size. The lowest energy is found in the smallest orbit.
• Radiation is absorbed or emitted when an electron moves from one orbit to another.

Bohr Model of Hydrogen

• The simplest example of the Bohr Model is for the hydrogen atom (Z = 1) or for a hydrogen-like ion (Z > 1), in which a negatively-charged electron orbits a small positively-charged nucleus. Electromagnetic energy will be absorbed or emitted if an electron moves from one orbit to another. Only certain electron orbits are permitted. The radius of the possible orbits increases as n2, where n is the principal quantum number. The 3 → 2 transition produces the first line of the Balmer series. For hydrogen (Z = 1) this produces a photon having wavelength 656 nm (red light).

• Problems with the Bohr Model

  • It violates the Heisenberg Uncertainty Principle because it considers electrons to have both a known radius and orbit.
  • The Bohr Model provides an incorrect value for the ground state orbital angular momentum.
  • It makes poor predictions regarding the spectra of larger atoms.
  • It does not predict the relative intensities of spectral lines.
  • The Bohr Model does not explain fine structure and hyperfine structure in spectral lines.
  • It does not explain the Zeeman Effect.

RUTHERFORD MODEL OF ATOM

Development of the Rutherford Model

In 1909, Rutherford conducted his famous gold foil experiment. In the experiment, Rutherford and his colleague Hans Geiger bombarded a piece of gold foil with positively charged alpha particles, expecting particles to travel straight through the foil. Instead, many alpha particles ricocheted off of the foil, suggesting that there was something positive these particles were colliding with. They named this positive force the nucleus. The Rutherford Model was created based on this new data.

The diagram above depicts the expected and the actual results of the gold foil experiment. The diagram on the left shows particles passing through the positively charged matrix of the plum pudding model. The diagram on the right shows a particle ricocheting off of the nucleus in the center of the atom.

J.J THOMSON MODEL OF ATOM

The Discovery of the Electron (J. J. Thomson)
In 1897, J. J. Thomson found that the cathode rays can be deflected by an electric field, as shown below. By balancing the effect of a magnetic field on a cathode-ray beam with an electric field, Thomson was able to show thatcathode "rays" are actually composed of particles. This experiment also provided an estimate of the ratio of the charge to the mass of these particles.
In the SI system, charge is measured in units of coulombs. By definition, one coulomb is the charge carried by a current of one ampere that flows for one second: 1 C = 1 amp-s. When Thomson's data are converted to SI units, the charge-to-mass ratio of the particles in the cathode-ray beam is about 10⁸ coulomb per gram.
Thomson found the same charge-to-mass ratio regardless of the metal used to make the cathode and the anode. He also found the same charge-to-mass ratio regardless of the gas used to fill the tube. He therefore concluded that the particles given off by the cathode in this experiment are a universal component of matter. Although Thomson called these particles corpuscles, the name electron, which had been proposed by George Stoney several years earlier for the fundamental unit of negative electricity, was soon accepted.

The cathode rays also can be delected by an electric field in a direction which suggests they are negatively charged.

The Raisin Pudding Model of the Atom (J. J. Thomson)
Thomson recognized one of the consequences of the discovery of the electron. Because matter is electrically neutral, there must be a positively charged particle that balances the negative charge on the electrons in an atom. Furthermore, if electrons are very much lighter than atoms, these positively charged particles must carry the mass of the atom. Thomson therefore suggested that atoms are spheres of positive charge in which light, negatively charged electrons are embedded, much as raisins might be embedded in the surface of a pudding.  At the time Thomson proposed this model, evidence for the existence of positively charged particles was available from cathode-ray tube experiments.

Thomson's Raisin Pudding Model

ATOMIC STRUCTURE

Fundamental Subatomic Particles

Particle	Symbol	Charge		Mass
electron	e-	-1		0.0005486 amu
proton	p+	+1		1.007276 amu
neutron	no	0		1.008665 amu

The number of protons, neutrons, and electrons in an atom can be determined from a set of simple rules.

• The number of protons in the nucleus of the atom is equal to the atomic number (Z).
• The number of electrons in a neutral atom is equal to the number of protons.
• The mass number of the atom (M) is equal to the sum of the number of protons and neutrons in the nucleus.
• The number of neutrons is equal to the difference between the mass number of the atom (M) and the atomic number (Z).

Examples: Let's determine the number of protons, neutrons, and electrons in the following isotopes.

12C

13C

14C

14N

The different isotopes of an element are identified by writing the mass number of the atom in the upper left corner of the symbol for the element. ¹²C, ¹³C, and ¹⁴C are isotopes of carbon (Z = 6) and therefore contain six protons. If the atoms are neutral, they also must contain six electrons. The only difference between these isotopes is the number of neutrons in the nucleus.

¹²C: 6 electrons, 6 protons, and 6 neutrons

¹³C: 6 electrons, 6 protons, and 7 neutrons

¹⁴C: 6 electrons, 6 protons, and 8 neutrons

NORMALITY

Normality Definition:Normality is a measure of concentration equal to the gram equivalent weight per liter of solution. Gram equivalent weight is the measure of the reactive capacity of a molecule.

The solution's role in the reaction determines the solution's normality.

For acid reactions, a 1 M H2SO4 solution will have a normality (N) of 2 N because 2 moles of H+ ions are present per liter of solution.

For sulfide precipitation reactions, where the SO4- ion is the important part, the same 1 M H2SO4 solution will have a normality of 1 N.

MOLE FRACTION

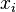In chemistry, the mole fraction or molar fraction () is defined as the amount of a constituent (expressed in moles), 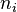, divided by the total amount of all constituents in a mixture, :

The sum of all the mole fractions is equal to 1:

The same concept expressed with a denominator of 100 is the mole percent or molar percentage or molar proportion(mol%).

The mole fraction is also called the amount fraction. It is identical to the number fraction, which is defined as the number of molecules of a constituent  divided by the total number of all molecules . The mole fraction is sometimes denoted by the lowercase Greek letter 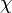 (chi) instead of a Roman . For mixtures of gases, IUPAC recommends the letter .

The National Institute of Standards and Technology of the United States prefers the term amount-of-substance fractionover mole fraction because it does not contain the name of the unit mole.

Whereas mole fraction is a ratio of moles to moles, molar concentration is a ratio of moles to volume.

The mole fraction is one way of expressing the composition of a mixture with a dimensionless quantity; mass fraction(percentage by weight, wt%) and volume fraction (percentage by volume, vol%) are others.

WHAT IS MOLALITY??

What Is Molality?

The concentration of a substance is a very important quantity in our daily lives. Household items like rubbing alcohol, mouthwash, bleach and various cleaning products can have various concentrations of their active ingredients. When we buy products, we sometimes take the concentration of the active ingredient into consideration, such as when buying an astringent: it is either 1% or 2% salicylic acid, so we make our choice based on how sensitive our skin is.

Chemists also have to be aware of the concentration of solutions they use during laboratory procedures. One of the ways concentration is expressed is through molality. Molality, symbolized by a small m, is the number of moles of solute per kilograms (kg) of solvent.

Formulas Needed for Problem Solving

The unit of molality is therefore expressed in mol/kg. The formula for molality is:

In problem solving involving molality, we sometimes need to use additional formulas to get to the final answer.

One formula we need to be aware of is the formula for density:

In molality, the unit is in moles of solute/kg of solvent. There are times when we are given the mass of the solvent in grams. To convert the mass from grams to kilograms, we use the conversion factor:

Sometimes, we are given the number of gramsof solute. Molality is the moles of solute per kg of solvent. To convert the number of grams of solute to moles of solute, we do the following:

To find the molar mass, we need to count the number of atoms for each element and get the sum of all the atomic masses of the atoms, from the periodic table, in the chemical compound.

Problem Solving: Molality

Let us go over a few examples of common problems encountered when we want to find the molality of a substance.

Example 1

What is the molality of a solution containing 0.75 moles of NaOH in 500 mL of water? The density of water is 1 g/mL.

Solution

WHAT IS MOLARITY??

Molarity is the concentration of a solution expressed as the number of moles ofsolute per litre of solution:

To get the molarity, you divide the moles of solute by the litres of solution.

Molarity=moles of solutelitres of solution

For example, a 0.25 mol/L NaOH solution contains 0.25 mol of sodium hydroxide in every litre of solution.

To calculate the molarity of a solution, you need to know the number of moles of solute and the total volume of the solution.

To calculate molarity:

1. Calculate the number of moles of solute present.
2. Calculate the number of litres of solution present.
3. Divide the number of moles of solute by the number of litres of solution.

EXAMPLE:

What is the molarity of a solution prepared by dissolving 15.0 g of NaOH in enough water to make a total of 225 mL of solution?

Solution:

1 mol of NaOH has a mass of 40.00 g, so

Moles of NaOH=15.0g NaOH×1 mol NaOH40.00g NaOH=0.375 mol NaOH

Litres of solution=225mL soln×1 L soln1000mL soln=0.225 L soln

Molarity=moles of solutelitres of solution=0.375 mol0.225 L=1.67 mol/L

Some students prefer to use a "molarity triangle".

labscience10ablock.wikispac

ANY PROBLEMS??

It summarizes the molarity formulas as

Moles=molarity × litres

Molarity=moleslitres

Litres=molesmolarity